ML estimator 是 Maximum Likelihood estimator (最有可能)
MMSE estimator 是 Minimum Mean Square Error estimator (最小平方誤差)
嚴格來說,ML estimation 是 classic estimation. MMSE 是 Bayesian estimation. 請另文參考。本文主要是以應用來比較。
這兩種 estimator 在實際應用上常遇到。 到底差異在那? 以及 when to apply what?
ML example: match filter (maximize decision SNR), digital communication detection (minimum BER- Bit Error Rate), etc. ML 一般是在 no prior information 時的最佳選擇。
MMSE example: Wiener filter (minimize error, maximize total SNR), Kalman filter (minimize error), etc. MMSE = min E(|x-x*|^2) 直譯為 minimum mean square. 通常 reserve 給 Bayesian estimation quardratic cost function with prior information.
簡單來說,ML estimator 主要應用是 estimate parameters based on what is most likely to create the oberved samples (但 parameter 本身 no prior information).
MMSE estimator 主要差別是 estimate waveform (Wiener filter) or sequences (Kalman filter) based on samples to minimize a cost function (mean square error function).
當然以上只是粗略的區分。也有 sequence ML estimator (Viterbi decoding algorithm 就是有名的例子)。反之 MMSE 也常用來 estimate parameters, 請 reference 前文 “Kalman filter: MMSE estimator”.
簡單例子 (類比通信和數位通信)
類比通信如 AM 或 FM, 接收時會被 noise 污染,理想的類比接收器就是 MMSE filter (如 Wiener filter), 儘可能還原原始的類比信號。實際上為了成本的考量,一般都用簡單的 LPF. ML estimator 在此就無用武之地。
數位通信如 PSK 或 FSK, 接收時也會被 noise 污染,但理想的接收器不是儘可能還原原始信號。如下圖所示,重點在 maximize decision moment 時的 SNR, 才能準確判斷收到是 0 or 1. 即使 waveform 有 distortion 也無妨,因為數位通信並不 care waveform. 理想的數位接收器就是 ML estimator (match filer), 能準確判斷收到(或送出)是 0 or 1. MMSE estimator and ML estimator 在這個例子顯然不同。
一個反例 (MMSE and ML estimator 相同結果): Linear Regression
==> 以下的例子並非是 MMSE, least square function or least square estimation (LSE) . 常常容易混淆 MMSE and least square optimzation, 以下誤導大家。
Least square estimation (LSE) and ML estimation 的差異可見本文。
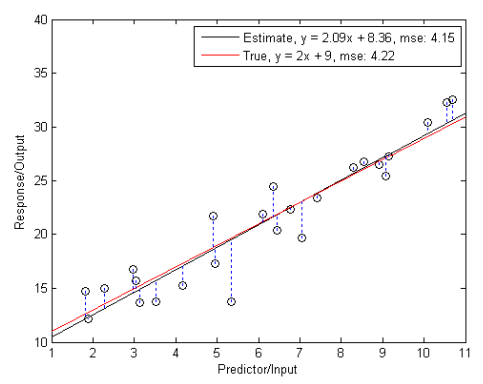
在 linear regression estimation, the goal is to estimate y = b_0 + b_1 x 中的 b_0 and b_1.
注意這是 estimate parameters b_0 and b_1, 不是如 Kalman filter estimate waveform.
先 define square error function 如下:
ML 的方法是先 define likelihood function 如下:
Then find what theta is most likely given Xi, i.e. find maximum of likelihood function.
更常用的是 log-likelihood function, take log of the likelihood function 再微分。
Assuming epi_i is Gaussian with i.i.d:
How to maximize the likelihood function? It tunrs out equivalent to minimize
以下為錯誤結論 :
In this case, MMSE and ML estimation are the same!!
到底 MMSE 和 ML 在 parameter estimation 有什麼不同,還是每次都會有相同的結果? 從上面的例子,MMSE estimator 和 error (epson_i) 的 pdf 沒有關係,但 ML estimator 明顯 depends on pdf.
舉例而言,如果 eps_i 不是 Gaussian, 而是 exponential distribution, ML 要 maximize likelihood function 就不會 equivalent to minimize “mean absolute error” (沒有 square).
In general, MMSE estimator 不管 error 的 pdf, 基本上只 care 1st order and 2nd order statistics (mean and variance). 換言之,就是假設 error pdf 是 Gaussian, MMSE estimator 就是 optimal estimator and achieve the Cramer-Rao lower bound (CRLB).
反之,ML estimator 會針對 error pdf (prior information) 做 optimization. 理論上會比 MMSE 更優? 如果 error pdf 是 Gaussian, MMSE and ML 就會得到相同的結果。
以下為正確的結論:
1. 上述 MMSE 應改為 least square estimation (LSE), 並沒有 mean (prior pdf) 的觀念。
2. ML estimator depends on pdf (稱為 likelihood function). 但 parameter 本身 no prior information.
3. Depending on the likelihood function, ML 需要 optimize 的 function 不同。For Gaussian likelihood function, 即為 least square function. For other likelihood function, 就會有不同的 minimal function.
另一個例子 (Sine Wave Estimation)
Sine wave estimation 有兩種 flavors: (i) Parameter estimation (假設 amplitude, frequency, phase are fixed); (ii) Waveform estimation (amplitude, frequency, phase can be time varying).
For (ii) waveform estimation, 很顯然只適合 MMSE estimator. For (i) parameter estimation, ML and MMSE 皆可用。
Sine Wave Parameter Estimation
這個例子在 digial signal processing 常常用到。Estimate 一個 sine wave 的頻率和 phase,不過這個 sine wave 被 additive Gaussian noise 所污染。這個問題有很多變形:sine wave 的 IQ imbalance; sine wave carrier synchronization; sine wave 包含了 harmonics; 或是 harmonic level 的 estimation, etc.
基本上有兩種做法:(i) Time domain or (ii) Frequency domain.
Time Domain Linear Method
Time domain method is mainly based on linear regression estimation. It shows accurate result at moderate to high SNRs.
Tretter suggests the following method:
以上 eq. (3), estimate wo and theta using x_t, t=0, 1, . ,N-1. 可以証明 ML estimator and MMSE estimator are equivalent. wo and theta are obtained by the equations in linear regression example.
There are two problems: (i) eq. (2) is only approximate model and accurate only at moderate to high SNRs.; (ii) (3) needs to do phase unwrapped and it can be error prone.
One variation of the sine wave estimation is coherent sampling. That is, the sampling frequency is integer multiple of the sine wave. In this case, the sine wave frequency is known, the only parameter to be estimated is the phase. Therefore, the phase is inversely proportional to the N^2.
The following is the math of problem statement, CRLB, and Tretter’s model
The following is the Tretter’s model.
Tretter’s algorithm involves unwrap(arctan) operation and achieve CRLB at a high SNR. It can be used for IQ imbalance estimation withour prior knowledge of the frequency. (IQ is arctan function).
In summary, Tretter’s algorithm
Pros: (i) No FFT, lower complexity; (ii) Sequence estimation, low latency
Cons: (ii) phase unwrap add additional complexity and may fail at low SNR
Kay improves the algorithm by using the differenced phase of two adjacent samples.
It is shown that Tretter and Kay’s algorithms are equivalent via Itoh’s phase unwrapping algorithm.
Time Domain Non-Linear Method
Zero crossing method, not surprising since arctan is nonlinear function. We can avoid the arctan by using zero crossing
Can it generalize to non-sine waveform? square wave or pulse like waveform? It may be useful for asynchronous eye diagram analysis???
Frequency Domain
D.C. Rife
Waveform example:
MMSE is used due to close resamble the original waveform!
It is NOT required to be a fixed sine wave. Some parameter could be time varying.
Example is like FM demodulation. How about zero crossing MMSE for FM demodulation?
A sin(wt + theta)
For MMSE estimator
For ML estimator, estimate A, w, or theta














沒有留言:
張貼留言