Quantum and Classic Physics

 

1. Start with classical Hamiltonia with p and x.  p and x are functions; p and x are circle in phaser diagram.  p and q are orthogonal!

2. Change p and x to operators on wave function and [p, x] = ih;   p and x are dependent!!!

3. p and q are conjugated base function.

4. Use harmonic oscillator as an example

5. All harmonic oscillation can be quantized into particle, phonon, photon, magnon, plasmon. etc.

 

Importance of Harmonic Oscillator

The quantum harmonic oscillator holds a unique importance in quantum mechanics, as it is both one
of the few problems that can really be solved in closed form, and is a very generally useful solution, both in
approximations and in exact solutions of various problems. 

Moreoever, it holds a key position in the 2nd quantization (wave/field) quantization since we can treat wave/field as multiple harmonic oscillators.

Classical Harmonic Oscillator

The classic harmonic oscillator is charaterized by Hamiltonia

  

Classical Coupled Oscillator

TBA

 

Quantum Harmonic Oscillator

The quantum harmonic oscillator is charaterized by the same Hamiltonia except H, P, X are now operators.

There are two ways to solve the quantum harmonic oscillator. 

(A) Solve the Schrodinger wave equation.  Refer to any quantum physics textbook.

(B) Use Dirac bracket (equivalent to Heisenburg uncertainty principle).  This leads to more profound insight!

 

Dirac Bracket

X and P are conjugated operators (base) that satifies

Let’s introduce the creation and annhilation operators a⁺ and a

a⁺ and a are not observables because they are not hermitians.

We can rewrite the Hamiltonia

with eigenvalues:

where

is an observable with eigenvalues n. 

 

Very important: harmonic oscillator is quantized and is equivalent to (or interpreted as) increase or decrease of bosons (hω).

H and have the same eigenstates (eigen functions).  These eigenstates |n> form a complete base and can be interpretated as n bosons.

 

when n=0

   

 

Classical vs. Quantum and Correspondence Principle

The probability of finding the object is different for classical and quantum oscillator.

For the classical case, the probability is greatest at the ends of the motion since it is moving more slowly and comes to rest instantaneously at the extremes of the motion. The relative probability of finding it is just the inverse of velocity.

For the quantum mechanical case the probability of finding the oscillator is the square of the wave function, and that is very different for the lower energy states as shown in figure below.

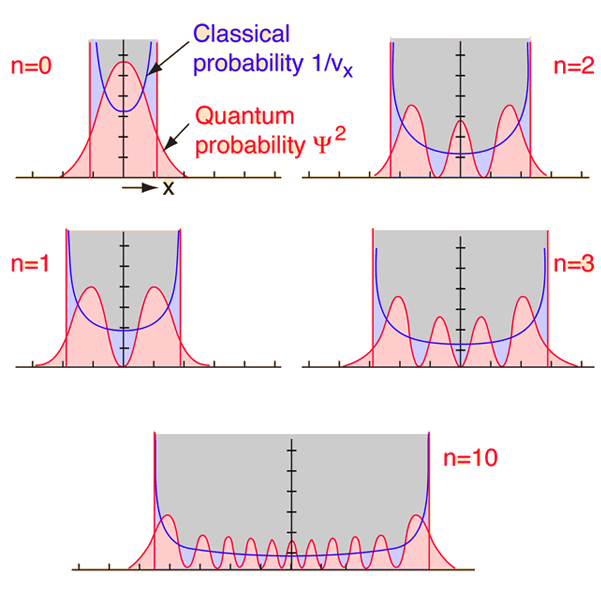
For n=0, classical and quantum harmonic oscillator are very different.  When the quantum number, n, increases, quantum treatment merges with classical oscillator.  This is in general true and Bohr called it “correspondence principle”.  There are exceptions such as black body radiation.   Beiser gives an example of calculating the radiation frequency of an atom for quantum number n=10,000 and states that it differs from the classical result by only 0.01%.  

 

N-Dimension (Uncoupled) Quantum Harmonic Oscillator

Therefore, N-dimension harmonic oscillator is just N times bosons compared with single harmonic oscillator.

Given n boson, the degeneracy is

 

For 3-D oscillator, g_n = (n+1)(n+2)/2.

 

N-Coupled Quantum Harmonic Oscillator

This is the key to extend harmonic oscillator to wave and field!

Because harmonic oscillator is quantized as boson (particle), wave and field can be quantized as collections of bosons.

The potential energy is summed over "nearest-neighbor" pairs, so there is one term for each spring.

Remarkably, there exists a coordinate transformation to turn this problem into N independent harmonic oscillators as discussed before, each of which corresponds to a particular collective distortion of the lattice.  These distortions display some particle-like properties.

        

 

There are difference between the coordinate transformed N coupled oscillator and N independent oscillator.

(i) ω_k is bounded (<2ω) and dispersive

 

(ii) Q_k and Π_k are not Hermitian.  Q_kQ_-k  and Π_kΠ_-k are Hermitan.

 

Quantum Harmonic Oscillator and Boson

Quantum harmonic oscillator is equivalent to create and annihil boson particles!  In other words, we can treate the quantum harmonic oscillator as collections of bosons with energy hω.  The more energy of the quantum oscillator, the more bosons it reprents.

馬上有兩個問題：(i) boson 是什麼形式;  (ii) boson 的數量和分佈 (based on |n> base functions)

(i)  What form the boson represents depending on the specific scenario

1. For a single electron, the boson seems to be a photon

2. For a atom, the boson can be a phonon or a photon

3. other examples

 

(ii) 數量和分佈 also depends on the specific scenario

1. For a coherent light source such as laser, it is in a coherent states with Poisson distribution

2. For a vibrating lattice with temperature T, the phonon distribution follows the Bose-Einstein distribution

Boltzmann distribution at high temperature; Debye derived the low temperature distribution.

 

 

 

 

 

treate EM wave as a string of rope, or using transmission line as model.  coupled harmonic oscillator.

 

can we treate discrete time and result electron spin??