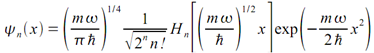1. Start with classical Hamiltonia with p and x. p and x are functions; p and x are circle in phaser diagram. p and q are orthogonal!
2. Change p and x to operators on wave function and [p, x] = ih; p and x are dependent!!!
3. p and q are conjugated base function.
4. Use harmonic oscillator as an example
5. All harmonic oscillation can be quantized into particle, phonon, photon, magnon, plasmon. etc.
Importance of Harmonic Oscillator
The quantum harmonic oscillator holds a unique importance in quantum mechanics, as it is both one
of the few problems that can really be solved in closed form, and is a very generally useful solution, both in
approximations and in exact solutions of various problems.
Moreoever, it holds a key position in the 2nd quantization (wave/field) quantization since we can treat wave/field as multiple harmonic oscillators.
Classical Harmonic Oscillator
The classic harmonic oscillator is charaterized by Hamiltonia
Classical Coupled Oscillator
TBA
Quantum Harmonic Oscillator
The quantum harmonic oscillator is charaterized by the same Hamiltonia except H, P, X are now operators.
There are two ways to solve the quantum harmonic oscillator.
(A) Solve the Schrodinger wave equation. Refer to any quantum physics textbook.
(B) Use Dirac bracket (equivalent to Heisenburg uncertainty principle). This leads to more profound insight!
Dirac Bracket
X and P are conjugated operators (base) that satifies
Let’s introduce the creation and annhilation operators a+ and a
a+ and a are not observables because they are not hermitians.
We can rewrite the Hamiltonia
with eigenvalues:
where
Very important: harmonic oscillator is quantized and is equivalent to (or interpreted as) increase or decrease of bosons (hω).
H and 
when n=0
Classical vs. Quantum and Correspondence Principle
The probability of finding the object is different for classical and quantum oscillator.
For the classical case, the probability is greatest at the ends of the motion since it is moving more slowly and comes to rest instantaneously at the extremes of the motion. The relative probability of finding it is just the inverse of velocity.
For the quantum mechanical case the probability of finding the oscillator is the square of the wave function, and that is very different for the lower energy states as shown in figure below.
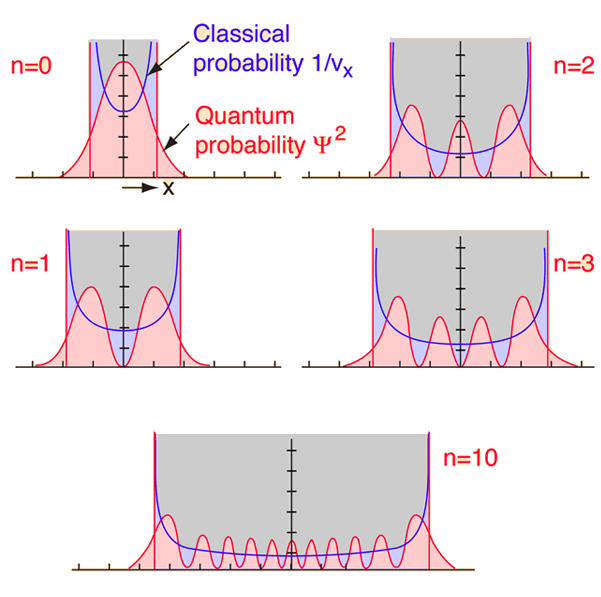
For n=0, classical and quantum harmonic oscillator are very different. When the quantum number, n, increases, quantum treatment merges with classical oscillator. This is in general true and Bohr called it “correspondence principle”. There are exceptions such as black body radiation. Beiser gives an example of calculating the radiation frequency of an atom for quantum number n=10,000 and states that it differs from the classical result by only 0.01%.
N-Dimension (Uncoupled) Quantum Harmonic Oscillator
Therefore, N-dimension harmonic oscillator is just N times bosons compared with single harmonic oscillator.
Given n boson, the degeneracy is
For 3-D oscillator, gn = (n+1)(n+2)/2.
N-Coupled Quantum Harmonic Oscillator
This is the key to extend harmonic oscillator to wave and field!
Because harmonic oscillator is quantized as boson (particle), wave and field can be quantized as collections of bosons.
The potential energy is summed over "nearest-neighbor" pairs, so there is one term for each spring.
Remarkably, there exists a coordinate transformation to turn this problem into N independent harmonic oscillators as discussed before, each of which corresponds to a particular collective distortion of the lattice. These distortions display some particle-like properties.
There are difference between the coordinate transformed N coupled oscillator and N independent oscillator.
(i) ωk is bounded (<2ω) and dispersive
(ii) Qk and Πk are not Hermitian. QkQ-k and ΠkΠ-k are Hermitan.
Quantum Harmonic Oscillator and Boson
Quantum harmonic oscillator is equivalent to create and annihil boson particles! In other words, we can treate the quantum harmonic oscillator as collections of bosons with energy hω. The more energy of the quantum oscillator, the more bosons it reprents.
馬上有兩個問題：(i) boson 是什麼形式; (ii) boson 的數量和分佈 (based on |n> base functions)
(i) What form the boson represents depending on the specific scenario
1. For a single electron, the boson seems to be a photon
2. For a atom, the boson can be a phonon or a photon
3. other examples
(ii) 數量和分佈 also depends on the specific scenario
1. For a coherent light source such as laser, it is in a coherent states with Poisson distribution
2. For a vibrating lattice with temperature T, the phonon distribution follows the Bose-Einstein distribution
Boltzmann distribution at high temperature; Debye derived the low temperature distribution.
treate EM wave as a string of rope, or using transmission line as model. coupled harmonic oscillator.
can we treate discrete time and result electron spin??
