多數人都不喜歡作虛功。但在古典力學中,虛功原理 (virtual work) 漂亮的洐生出 D'Alembert 原理,以及等價的最小作用原理。後者成為 Lagrangian mechanics 和 Hamiltonian mechanics 的基礎。可以說虛功原理簡單且容易了解,並不是真的作虛功。
什麼是虛功
Wiki 的定義如下。基本上是從牛頓力學第一定律出發導出虛功原理:
Consider a system of particles, i, in static equilibrium. Based on Newton's first law, the total force on each particle is
 .
.
Summing the work exerted by the force on each particle that acts through an arbitrary virtual displacement,  , of the system leads to an expression for the virtual work that must be zero since the forces are zero.
, of the system leads to an expression for the virtual work that must be zero since the forces are zero.
 .
.
At this point it should be noted that the original vector equation could be recovered by recognizing that the work expression must hold for arbitrary displacements. Separating the forces into applied forces, 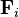 , and constraint forces,
, and constraint forces,  , yields
, yields
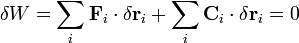 .
.
If arbitrary virtual displacements are assumed to be in directions that are orthogonal to the constraint forces, the constraint forces do no work. Such displacements are said to be consistent with the constraints. This leads to the formulation of the principle of virtual work for applied forces, which states that forces applied to a static system do no virtual work
 .
.
虛功原理源起於靜力學。它的白話文:對於一個處於平衡 (equilibrium, 一般為靜止)的系統,其外力乘上虛位移 (virtual displacement)為零。虛位移並不是任意的方向,而必須根據 constraint 的限制。
Lancos 則有不同的看法,他把虛功原理視為一個假設。配合牛頓第二定律可以推廣至動力學的 D'Alembert 原理。而與最小作用原理是等價。
虛功原理的應用
第一個重要的應用就是最低勢能原理。如果所有的外力都是勢能 (potential or work function) 的 derivative dV = -dU = F. dr = 0 , 虛功原理就變為靜力學的最低勢能原理 (minimal potential)。請參閱另一文章。
應用在 rigid body
應用在 rigid body
應用在 deformable body
應用在 incomperssible fluid
Pascal principle
differnce between Newtonian
minimal potential principle
difference between least action and virtue work
Virtual work does not depend on time (t), only a spacial function
Q: When virtue work equals to Newtonian law?
Q:
沒有留言:
張貼留言