Group Theory–我的經驗

前前後後花了後次時間自習 group theory,  每次都像是新的開始，之前學的統統忘了。前一兩次是 algebra approach, 從 definition (group/ring/field), more definitions (abelian, subgroup, normal subgroup, coset, conjugate, homophism, autohomophism, direct product, …), and theory (Lagrange, Sylow, Galois, …).  學的迷迷糊糊，因為從來用不到，最後統統忘掉。

再來是從 permutation 著手，搭配 Rubik cube, puzzle-15, etc. game 方面的應用，依然不得要領。

比較起來， linear algebra 雖然也很抽象, 但因為比較常用 (eigenvalue, eigenfucntion)，倒不致於完全忘光。

最近從 geometry symmetry 著手，開始比較有一些感覺。如 cyclic group, dihedral group, symmetry group.  不過也止於一些 geometry 的對稱群，沒有更深的領悟。無法和之前 algebra approach 的一堆 definition 和 theory link 在一起。

這次看了 Carter 的 visual group theory 的 video, 非常有感覺。Carter 用 Cayley diagram visualize symmetry，同時用 Cayley diagram 來解釋 group product, normal subgroup, quotient group.  One picture more than a thousand words!    http://web.bentley.edu/empl/c/ncarter/vgt/index.html   另外YouTube 和 Google book 都有相關的資料。

 

Cayley Graph

Group theory visualization 的根本是 Cayley graph (or Cayley diagram).  Cayley diagram 包含兩個部份：node 表示 group element.  Arrow 表示 group generator 的作用。

數學上的定義請參考：http://en.wikipedia.org/wiki/Cayley_graph

我們的重點是如何用 Cayley graph  直覺式的看穿 group 的結構和理解 group theory 中的 definition 和 theory。

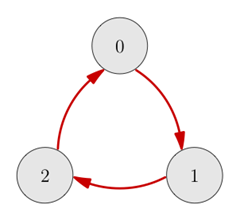
以下的一個例子是一個簡單的化學分子，有三個 branch。它的對應 Cayley graph 如右。Generator 是一個 120 度順時針旋轉，每一次的操作都保持原來的形狀。在 group theory 中這是一個 cyclic group with order 3, or C₃ group。

                              

 

常見的對稱 Group 以及 Cayley Graph

Cyclic Group, C_n : 看圖就可以理解這是旋轉對稱所對應的 group 和 Cayley graph.

 

 

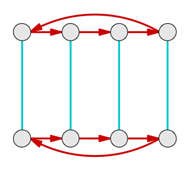
Dihedral Group, D_n : 下圖是正三角型所有的對稱操作，也稱為 D₃ group。 D_n group (正 n 邊型/regular polygon) 包含了旋轉對稱+鏡像對稱，比起單純的 cyclic group 多了鏡像對稱。因此 D_n group Cayley graph 中的 node 多了一倍。D_n group 有兩種 generators, 對應旋轉對稱和鏡像對稱。兩種 geneator 的 arrows, 分別用 green 和 blue arrows 來表示。鏡像對稱是正->負-> 正->負.. 因此 arrow 是雙向的，圖中就省略了雙向箭頭。

D_n group 的 Caley graph 如下。光看 Cayley graph 就知道 D_n group 是 non-abelian group, why?

 

Abelian Group :  Abelian group 的特點是所有的 group element 符合 commutating rule, ab = ba.  Non-abelian group 在 quantum physics 扮演了關鍵的角色，例如 Yang-Mills theory.  

從 Cayley graph 可以容易的判斷是否為 Abelian group.  我們可以証明 group element commutes 等同於 group generator commute.  如果只有一個 generator, 如 cyclic group, 一定是 Abelian group.  兩個 generator 以上，可以用下圖來判別。如果所有不同顏色的 arrow 交換都指到同一個 node, 是 Abelian group.  只要有任何 arrow 交換指到不同的 node, 則是 non-abelian group.   所以上述的 dihedral group 是 non-abelian group. 

 

 

除了 cyclic group 以外，下列各圖都是 Abelian group

     

相反的，以下都是 non-abelian group.

        

由圖就可以看出來，Abelian group 都是 grid 的結構。所有的 arrows 都是垂直或水平 (除了端點的 arrow 要繞回另一端外)。Non-abelian group 的 arrow 則非直角或相互交錯。.

 

Symmetric Group and Alternating Group,  S_n or  A_n 

Dihedral group 表徵兩維平面的正多邊型的對稱。對於三維空間的正多面體 ( 如正三角錐，cube, etc.  i.e. regular polyhedron)，顯然有更多的對稱操作。它們對應的對稱 group 為 symmetric group 和 alternating group.

Symmetric group, S_n : 包含 n! permutation (S3:6, S4:24, S5:120, …).  S3 = D3

Alternating group, A_n : 包含 n!/2 even permulation (A4:12, A5:60, …)

Tetrahedron: 有兩種對稱操作? (都是面旋轉120度?)。12 個 node, 是 A4 group

Cube: 有旋轉對稱和鏡像對稱。24 (8x3) node, 是 S4 group

Octahedron : 有旋轉對稱和鏡像對稱。24 (4x6) node, 是 S4 group

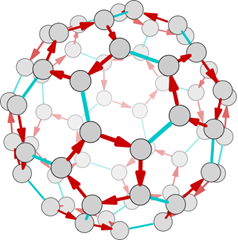
Dodecahedron : 60 node, 是 A5 group

 

Icosahedron :  60 node, 是 A5 group

 

除了上述五種正多面體以外，不存在更多的正多面體，這是古希臘人就已經知道的事。意即不存在 S₅ (含) 以上正多面體的對稱群。這和 5 次方程式(含)以上無根式解有密切的關係，Galois 就是有此洞見而創建了 group theory。S5 (含) 以上的 symmetric group 也稱為 non-solvable symmetry group.