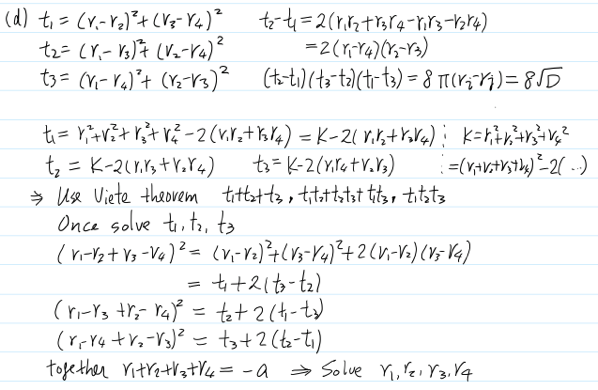不用現代代數的 Galois Theory

現代代數在解釋 Galois Theory 大多是用 field/group 的 automorphism 和  homomorphism 解釋。

雖然簡潔優美，但缺乏直覺。其實 Galois 本身的思路是比較直覺容易理解。

前文提到結城浩的數學女孩就是 follow Galois 思路。雖然寫得很好，不過還是有些避重就輕。

雖然有解釋 Galois 的思路，但嚴謹度缺乏而顯得破碎。另一方面是缺少有分量的範例。

數學女孩大多用二次式來解釋。間或有三次以及四次的一些推論，但沒有札實的例子。

 

偏偏二次式是非常簡單的 case.  很難直觀推論到三次, 四次, 或五次方程式。

下文則是非常好的介紹文:  Galois theory without abstract algebra.  也是同樣用 Galois 原來的思路。

同時輔佐實際的 2, 3, 4, 5 次式例子。即使五次式沒有通解。但 F20 group 仍存在根式解。

 

首先定義有理多項式(方程式)的根式解。如下:

A, B, C, D, 以及 a, b, c, .. 都是有理數。這是所謂的根式解。

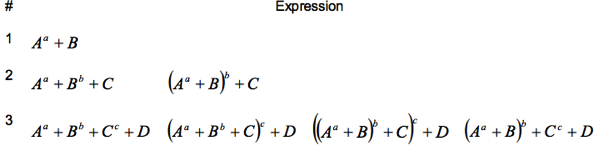
二次式 x^2 + 2bx + c = 0 的根式解就是 1.  A = b² - c;  B = -b;  a = 1/2

三次式的根式解就是 2. 或是 2. 的 linear combination.

依此類推。

前文有提過上述根式解的數，都可以找到對應有理係數多項式的根。因此稱為代數數。

代數數的定義就是有理係數多項式的根。但並非所有代數數都可以

 

再來是定義 elementary symmetric polynomial

Elementary symmetric polynomial 就是把 (x+r₁)(x+r₂)(x+r₃) ... (x+r_n) 展開，根據 xⁱ  項歸類所得的係數。

For example:

(x+r₁)(x+r₂) = x² + σ₁ x + σ₂   where σ₁ = r₁ + r₂ ;  σ₂ = r_{1 *} r₂ 

對於高次多項式:

同時如果定義 

 

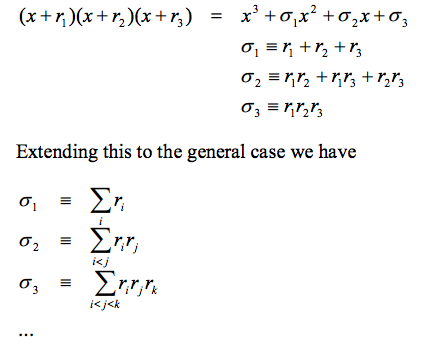
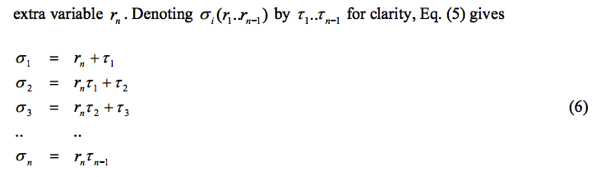
注意以上的公式適用於所有實數和複數，並無有理數的限制。

我們有興趣的 case 是有理數係數的多項式。當然根可能是或非有理數。但上述公式告訴我們。

根的 "基本對稱多項式" 如 σ_i 是有理數!  這是很直接但非常重要的觀察結果。

 

 

這個推論 (有理係數多項式的根所構成的基本對稱對項式是有理數) 能 extend 多遠?  

相當遠!  可以証明任意有理對稱多項式滿足 S_n permutation invariant 結果都是有理數。同時可以表示為 σ_i 的有理式!

是用數學歸納法証明。

 

n=1 :  σ₁ = r₁ ∈ Q.  任意有理(對稱)多項式 f(r₁) = f(σ₁) ∈ Q.   明顯成立。

 

假設 n-1 成立:

i.e. 任何有理多項式  f(r₁, r₂, ..., r_n-1) = g(σ₁, σ₂, ..., σ_n-1)  where f(r₁, r₂, ..., r_n-1) is invariant under S_n-1 permutation

 

Prove n: for any rational symmetry polynomial f(r₁, r₂, ..., r_n-1, r_n) satisfy S_n permutation invariant. 

First set r_n = 0. 

f(r₁, r₂, ..., r_n-1, r_n) = f(r₁, r₂, ..., r_n-1, 0)  當然仍然滿足 S_n-1 permutation invariant. 

By n-1 assumption,  f(r₁, r₂, ..., r_n-1, r_n=0) = f(r₁, r₂, ..., r_n-1, 0) = g(σ₁, σ₂, ..., σ_n-1, σ_n=0)  from (6)

=>  [f(r₁, r₂, ..., r_n-1, r_n) - g(σ₁, σ₂, ..., σ_n-1, σ_n)]_rn=0 = 0  也就是 r_n 是一個根。同理 r₁, r₂, ..., r_n-1 都是根。

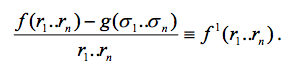
Clearly,  f ¹(r₁, r₂, ..., r_n-1, r_n) is invariant under Sn permutation.  同時比原來的 f 更低階。

我們可以重覆這個 operation.  一直到 f ^k(r₁, r₂, ..., r_n-1, r_n) = g(σ₁, σ₂, ..., σ_n-1, σ_n)

In summary

任意有理對稱多項式滿足 S_n permutation invariant 結果都是有理數。

同時可以表示為 σ_i (基本對稱多項式)的有理式!

 

Galois Group

Maximum group of roots permutation invariant under any function.  The result is a known function of polynomial coefficients.

 

Example:

二次式 (roots: r1, r2):

σ₁ = r₁ + r₂  ,    t² = (r₁ - r₂)²  ∈ Q    σ₁ and t ∈ S2.  t 開根號後可以計算 r1 and r2.

結果就是一開始的根式解。

至於 Galois group:

S2=C2=Z2 ⊳ E   (The quotient group is Z2)

 

三次式 (roots: r1, r2, r3):

 

where α2 = ω, α3 = ω*ω

t1^3 is permutation invariant under A3.  t2^3 is also permutation invariant under A3.

但是 t1^3+t2^3 and t1^3*t2^3 則是 permutation invariant under S3.   

=> t1^3+t2^3, t1^3*t2^3 ∈ Q  =>  可以解出 t1 and t2 first. 

=> 再由 t1 and t2 解出 r1, r2, and r3 by (15).

如何找 t1^3 and t2^3?  就是展開上式利用根和係數得到 t1^3+t2^3 and t1^3*t2^3

 

S3 ⊳ A3=C3=Z3 ⊳ E   (The quotient group is Z2, and Z3, respectively)

 

四次式:

 

S4(24) ⊳ A4(12) ⊳ D2(4)=V4(4)=C2xC2 ⊳ C2=Z2(2) ⊳ E   (The quotient group is Z2, Z3, Z2, and Z2 respectively)

同樣可以先解出

 

如同三次式的 t1^3 and t2^3!  當然 θ1 and θ2 滿足 A4 permutation invariant.

所以 θ1+θ2 和 (θ1-θ2)^2 滿足 S4 permuation invariant. 

 

下一步就是要找到對應的 θ1 and θ2, 必須滿足 A4 permutation invariant. 

 

(t1 + ω t2 + ω^2 t3)^3 = θ1    

(t2 + ω t1 + ω^2 t3)^3 = θ2

(t1 + ω t3 + ω^2 t2)^3 = θ3  same as θ2, useless

t1 + t2 + t3 =?

看來只有 A3 permutation invariant? 

但 t1, t2, and t3 不是四次式的根。而是三次式的根。不過是什麼三次式的根?

答案是 it depends:

 

如果定義 (a)

t1 = (r1+r2)(r3+r4)

t2 = (r1+r3)(r2+r4)  

t3 = (r1+r4)(r2+r3)

可以得出一個三次式。

也可以定義 (b)

t1 = r1*r2 + r3*r4

t2 = r1*r3 + r2*r4  

t3 = r1*r4 + r2*r3

可以得出另一個三次式。

或是定義 (c)

t1 = [(r1-r2)(r3-r4)]^2

t2 = [(r1-r3)(r2-r4)]^2  

t3 = [(r1-r4)(r2-r3)]^2

可以得出另一個三次式。

或是定義 (d)

t1 = (r1-r2)^2 + (r3-r4)^2 = (r1-r2+ i r3 - i r4)*(r1-r2- i r3 + i r4) = (r1+ i*r3 -r2 - i*r4)(r1+ i*r4 -r2 - i*r3)

t2 = (r1-r3)^2 + (r2-r4)^2 = (r1-r3+ i r2 - i r4)*(r1-r3- i r2 + i r4) = (r1+ i*r2 -r3 - i*r4)(r1+ i*r4 -r3 - i*r2)

t3 = (r1-r4)^2 + (r2-r3)^2 = (r1-r4+ i r2 - i r3)*(r1-r4- i r2 + i r3) = (r1+ i*r2 -r4 - i*r3)(r1+ i*r3 -r4 - i*r2)

 

可以得出另一個三次式。

 

共同的特點 t1, t2, t3 都滿足 V8 (8) permutation invariant.  Total 8*3 = 24 permutation 構成 S4 permutation invariant for t1+t2+t3, t1*t2+t2*t3+t3*t1, and t1*t2*t3.

藉著 S4 permutation invariant 代表三次方程式的係數都可由四次方程式的係數表示。

最常用的是 (a).  可以參考本文 for 三次式的 coefficient. 

 

如果是 (d), 可以定義類似四次分圓根 (1,i,-1,-i) 的關係。

z1  = r1 + i r2 - r3 - i r4

z1' = r1 + i r4 - r3 - i r2 

z2  = r3 + i r2 - r1 - i r4

z2' = r3 + i r4 - r1 - i r2

z3  = r2 + i r1 - r4 - i r3

z3' = r2 + i r3 - r4 - i r1 

z4  = r4 + i r1 - r2 - i r3

z4' = r4 + i r3 - r2 - i r1

z1*z1' = z2*z2' = z3*z3' = z4*z4' = t1

同樣可以定義 t2 and t3.

 

t1+t2+t3 = (r1-r2)^2 + (r2-r3)^2 + (r3-r4)^2 + (r1-r3)^2 + (r1-r4)^2 + (r2-r4)^2

= 3*(r1+r2+r3+r4)^2 - 8*(r1r2+r1r3+r1r4+r2r3+r2r4+r3r4)

t1*t2+t2*t3+t1*t3 and t1*t2*t3 就要再計算。此處忽略。

 

先以 (a) 定義的三次多項式來看。

首先三次多項式的 D 和四次多項式的 D 是一致。其實 (a),(b),(c),(d) 都一致。

另外就是三次多項是否是 reducible?  也就是是否有有理根。

t1 = (r1+r2)(r3+r4) 

r1+r2+r3+r4 = -a    --- (1)

=> (r1+r2 - r3 - r4)^2 = a^2 - 4*t1

r1 + r2 - r3 - r4 = +/-sqrt(a^2 - 4*t1)   --- (2)

r1 + r3 - r2 - r4 = +/-sqrt(a^2 - 4*t2)   --- (3)

r1 + r4 - r2 - r3 = +/-sqrt(a^2 - 4*t3)   --- (4)

 

From (1) to (4), we can solve r1, r2, r3, r4 unknowns.

也可以先解: r1+r2, r3+r4, r1+r3, r2+r4, r1+r4, r2+r3

從 r1+r2 只要有 r1-r2 就可解 r1, r2.   r1-r2 = (r1+r3) - (r2+r3)

最後可解 r1, r2, r3, r4. 

 

所以順序上是先解 θ1 and θ2.  ( S4(24) ⊳ A4(12) )

再解 t1, t2, t3.  ( A4(12) ⊳ V4(4)  or S4(24) ⊳ V8(8) )

再解 r1+r2, r1+r3, r1+r4, r2+r3, r2+r4, r3+r4 ( V8(8) ⊳ C2(2) )

最後再解 C2(2) ⊳ E

 

-a3 = (r1+r2)+(r3+r4)

d1 = r1+r2 - (r3+r4)         (12)(34)

d2 = (r1+r3) - (r2+r4)

d3 = (r1+r4) - (r2+r3)

 

(a3^2 - d1^2)/4  =  (r1+r2)(r3+r4) = t1

(a3^2 - d2^2)/4  =  (r1+r3)(r2+r4) = t2

(a3^2 - d3^2)/4  =  (r1+r4)(r2+r3) = t3

 

實務上先做出一個三次方程預解式，使用 t1, t2, t3 為根。