Smith Chart

Introduction

Maxwell published his famous equations governing all electrical and electronic phenomenon (with some quantum mechanics in some cases) in 1873.  There are two problems.  First, the math of solving the Maxwell equation consists of vector analysis and partial differential equation.  It is too cubersome to derive the solution of a particular problem.

It seems that there is a dilemma to get a full picture of a simple dipole antenna.  Solving Maxwell equations provides the accurate solution, but loses the physical intuition and not practical due to the computation complexity. 

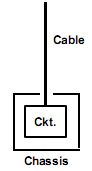
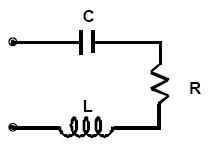
Lumped circuit model provides a simple approximation of a dipole antenna, it is useful but only valid within limited frequency range.  The situation is shown in Fig. 6.

Fig. 6: Different abstraction in electrical discipline

Luckily, there is a another tool originally derived from transmission line, namely Smith Chart, provides useful physical insight and enough accuracy for understanding the dipole antenna.  A brief introduction of Smith Chart is on the other article.  Lumped circuit is a subset included in Smith Chart.  Smith Chart (transmission line) is based on a specific EM wave called TEM (transverse EM) wave where the dynamic electrical and magnetic fields are perpendicular to the wave propagation direction.  The majority of EM wave and waveguide either belong to the TEM domain or can be approximated by TEM wave.  That is, Smith Chart is a very useful tool to solve most electrical problems.

 

The Smith Chart is plotted on the complex reflection coefficient plane in two dimensions and is scaled in normalized impedance (the most common), normalized admittance or both.  Normalized scaling allows the Smith Chart to be used for problems involving any characteristic impedance or system impedance, although by far the most commonly used is 50 Ohm.  With relatively simple graphical construction it is straightforward to convert between normalized impedance and the corresponding complex voltage reflection coefficient.  Please refer wiki's Smart Chart for details and this reference.

How Smith Chart Work?

The keys are complex reflection coefficient, G, and normalized impedance, z, are plotted on the same chart as shown in Figure 1. 

• The red x-y aisles represents the real and imaginary part of G.  The intersecting point is the origin of the Smith Chart.  Because |G| <= 1, the Smith Chart is fit inside a unit circle.  The Smith Chart is not suitable for active circuit where the reflection coefficient might be larger than 1.     
• The green circles represent zr = constant (zr is the real part of normalized impedance).  The constant must be positive.  The largest circle corresponds to zr=0 and also |G|=1.  As zr increases to infinity, the circle converges to a point G=1 that is a open load.   
• The black circles represents zi = constant (zi the imaginary part of normalized impedance).  The constant can be positive/inductive, circles on the upper plane; or negative/capacitive,  circles on the lower plane.  The largest circle, x-axis,  corresponds to zi=0.  As zi increases to both positive/negative infinity, the circles also converges to a point G=1 that is a open load.     

 

Fig. 1: Smith Chart Fundamental

 

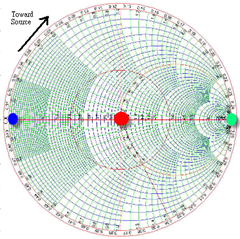
Fig. 2: Smith Chart

• The red-dot in Fig. 2 corresponds to no reflection (50Ohm load, G=0) ; the blue-dot corresponds to short load (G=-1); the green-dot corresponds to open load (G=1).  The open load and short load is mirrored to each other through l/4 transformation as discussed in the next section.

Example:

Assume the characteristic impedance is 50Ω :

Z₁ = 100 + j50Ω    Z₂ = 75 - j100Ω    Z₃ = j200Ω
Z₄ = 150Ω  Z₅ = ∞ (open)   Z₆ = 0 (short)
Z₇ = 50Ω   Z₈ = 184 - j900Ω

 

Fig. 3: Some Example Impedance

Note that a dipole antenna is close to open (Z5) at DC and becomes capacitive at lower frequency (Z8).  If it is well matched at operating frequency, the impedance is close to 50Ohm (Z7); that is: Z5->Z8->Z2->Z7.  Practically, the trajectory may be similar to the purple area because of non-perfect matching.

 

Transmission Line on Smith Chart

 

Fig. 4: Input Impedance with Transmission Line

One key advantage of Smith Chart is to obtain the input impedance of a load with transmission line shown in the above figure. 

• For a lossless transmission line, the input impedance toward source is simply a clockwise rotation of the load impedance on the Smith Chart shown in Fig. 2.  To remember clockwise rotation is to observe open load (green-dot) turns to capacitive (negative) load first; or short load (blue-dot) turns to inductive (positive) load first.
• One full circle rotation on Smith Chart represents half-wavelength (l/2) transmission line length; half circle rotation represents l/4 line length.  Remember the famous quarter wavelength impedance transformation.  From open to short is half circle rotation, corresponds to l/4 transmission line length.  For any load after the l/4 transformation, the input impedance becomes the mirror point (with origin) on the Smith Chart.

Even though the Smith Chart is developed for system with transmission line, it is also very useful in lumped circuit for matching and analysis purpose in RF IC design  shown in next sections.

 

Admittance Smith Chart

The Smith chart is built by considering impedance (resistor and reactance).  Once the Smith chart is built, it can be used to analyze these parameters in both the series and parallel worlds.  Adding elements in a series is straightforward.  New elements can be added and their effects determined by simply moving along the circle to their respective values.  However, summing elements in parallel is another matter.  This requires considering additional parameters.  Often it is easier to work with parallel elements in the admittance world.

It turns out that the expression for y is the opposite, in sign, of z, and Γ(y) = -Γ(z).  If we know z, we can invert the signs of Γ and find a mirror point situated in the opposite direction.   Thus, an admittance Smith chart can be obtained by rotating the whole impedance Smith chart by 180°.  This is extremely convenient, as it eliminates the necessity of building another chart.  The intersecting point of all the circles (constant conductance and constant susceptances) is at the point (-1, 0) automatically.  With that plot, adding elements in parallel also becomes easier.  Math details can refer to this.

 

Lumped Elements on Smith Chart

When solving problems where elements in series and in parallel are mixed together, we can use the same Smith chart and rotate it around any point where conversions from z to y or y to z exist. 

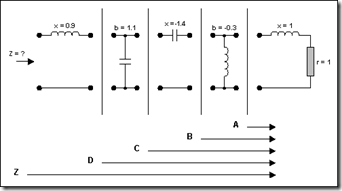
Let's consider the network of Fig. 5 (the elements are normalized with Z₀ = 50Ω).  The series reactance (x) is positive for inductance and negative for capacitance. The susceptance (b) is positive for capacitance and negative for inductance.

 

Fig. 5: Input Impedance of Lumped Elements

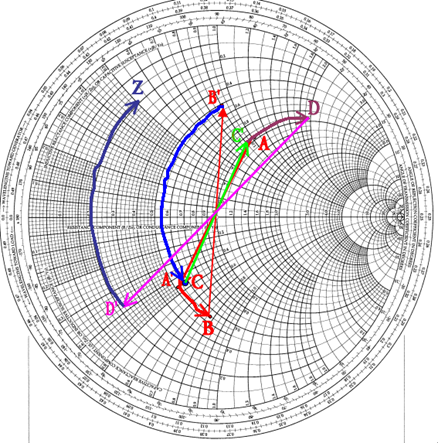
The circuit needs to be simplified (see Fig. 6).  Starting at the right side, where there is a resistor and an inductor with a value of 1, we plot a series point where the r circle = 1 and the l circle = 1.  This becomes point A.  As the next element is an element in shunt (parallel), we switch to the admittance Smith chart (by rotating the whole plane 180°).  To do this, however, we need to convert the previous point into admittance.  This becomes A'.  We then rotate the plane by 180°.  We are now in the admittance mode.  The shunt element can be added by going along the conductance circle by a distance corresponding to 0.3.  This must be done in a counterclockwise direction (negative value) and gives point B.  Fig. 7 shows the complete impedance transformation using Smith Chart.

Fig. 6: Break the Network for Analysis

Fig. 7: Impedance Using Smith Chart

 

In summary

1. Add a serial L:

Move up (clockwise) along  r=constant circle (circles intersects at (1,0))

2. Add a shunt L:

Move up (counter-clock) along g=constant circle (circles intersects at (-1,0))

3. Add a serial C:

Move down (counterclockwise) along r=constant circle (circles intersects at (1,0))

4. Add a shunt C:

Move  down (clockwise) along g=constant circle (circles intersects at (-1,0))

The following figure shows the summary.

 

 

How to do matching using Smith Chart

L-match (8 types)

The following figure shows 4 different type of L match for positive reactance matching

 

 

Similarly, there are 4 types for negative reactance just exchange L and C.

pi/T-match

 

There are above 8 types of pi/T matching.  Similarly, the mirror from positive to negative is to change L and C.

 

Examples

(I) Impedance Transformation from Tom Lee's RF CMOS book.

* If ZL is a pure resistance and ZL > Zo; only type2 (shunt-C with serial-L, or shunt-L with serial C) can convert Zin < ZL and Zin = ZL / ??  (only at resonant frequency, normally is a LPF or  HPF)

* If ZL is a pure resistance and ZL < Zo; only type 4 (serial-C with shunt-L, or  serial C with shunt C) can convert Zin > ZL and Zin = ?? (only at resonant frequency, normally is a HPF)

The above two L matches are in Tom Lee's book.

(II)

For dipole antenna below resonating frequency, it is like a serial RLC resonator; the resistor is higher than 50Ohm (air is 270Ohm); typical may be  75Ohm.  The resonating  frequency is assumed to be higher than the desired frequency.   (Example, the LC frequency maybe 1GHz, but the operating frequency is 600MHz, etc.) 

Therefore, the impedance is  75+X j Ohm (X is -200 to -50 Ohm).  Is it possible to design a matching network? 

Before/after resonating frequency

Condition 1: Re > 50Ohm and Im < 0 (capacitive load with high real impedance): example: dipole antenna before resonator

Condition 2: Re < 50Ohm and Im > 0 (inductive load and low real impedance): example: loop antenna

Condition 3: Re > 50Ohm and Im > 0 (inductive load with high real impedance??): example: dipole antenna after the resonator?

Condition 4: Re < 50Ohm and Im < 0 (capacitive load with low real impedance??): example: loop antenna

The matching choice (a) serial inductor; (b) parallel inductor.  Both reduce the reactive part.  The problem of (a) is real part is not change.  Therefore choose (b) to reduce R from 72 to 50.  Then use a serial capacitor to bring to the right matching point!!!

The best way to do is to use the center frequency first, not considering the entire frequency range.  E.g. 400M to 800M, maybe use 600M for the matching purpose!!

Examine the L and Pi match

Impedance Matching with Smart Chart

http://www.maxim-ic.com/appnotes.cfm/an_pk/742/

• Match for maximum power transfer or optimize the noise figure or highest gain?  Highest gain is always lowest noise figure?
• Maximum power transfer => Rs = RL*
• ?Ensure quality factor impact or access stability analysis because the matching network can be LPF or HPF or BPF.
• ? Can we replace RLC with scattering wave analysis using smith chart for both passive and active component (cmos?)  there is no concept of impedance at low frequency? wrong, can I still normalize to 50Ohm since there is still finite value of impedance?

雙極(dipole)和單極(monopole)天線簡介

天線在今日的電子產品的角色日益重要。一方面由於無線產品越來越普及，各式的手機、GPS、藍牙耳機及週邊都會需要靈敏及內建的天線。另一方面，高速的電路如果不注意，會有意想不到的天線耦合效應而干擾其他電子產品，造成 EMI 或 EMC 的間題而影響產品的認証和量產。

本文介紹最簡單且普遍的天線：雙極及單極天線 (dipole and monopole antenna)。簡單是因為它的數學及物理特性；普遍是因為它的設計和成本而有廣泛應用。同時雙極和單極天線所得到的結果可用於其他更複雜的天線上。

雙極天線的結構和原理

Fig. 1a 草繪了一個雙極天線。基本上就是兩根金屬線指向相反方向。極性相反的電流由中間流入(出)兩根金屬線形成雙極天線。如果從電路學來看，可能難以理解電流如何流入(出)完全斷開的金屬線。這可用 Fig. 1b 的虛擬電容 (virtue capacitance) 來 model 及解釋。這個虛擬電容把斷路的雙極電線變為一個迴路，可以用電路理論來了解天線的特性，而不用更複雜的電磁場理論。

這個虛擬電容包含了少部份的寄生電容 (parasitic capacitance) 以及大部份儲存電場能量的等效電容。

雙極天線的優點：

不需要 ground, 同時也比較不受環境影響(人體等等)，常用於早期類比電視的天線或外接天級(如 Fig. 1c 用於 Mio 和 Panasonic 數位電視的外接天線）。

雙極天線的缺點：所佔的空間較大，少用於小型電子產品例如手機、行動電視等。

 

Fig. 1a and 1b

Fig. 1c 外接雙極天線

一個簡單的類比是拍手，需要兩隻手（雙極）才能拍出聲音（電磁波）。

 

單極天線的結構和原理

故名思義單極天線只有一根金屬線，Fig. 2a 草繪了一個單極天線。從電磁學理論，天線能夠發射或接收 RF 訊號，需要有電位差 (potential difference)，才能形成電磁波（或電流形成迴路)。因此仍要一個參考面如 Fig. 2a 所示，通常參考面是電路板的 ground 或機殼 ground。如果沒有提供參考面，單極天線會自動找到參考面，通常是天線附近最大的導體就自動形成迴路，不一定是 ground包含，甚至人體也可以。不過人體並不是很穩定的參考面，因此單極天線若是沒有很好的參考面，常常會因為人體的接近影響收訊 (如 FM 天線)。 數位電視的外接單極天線一般會有穩定的參考面，但是內建的單極天線也常常會有穩定性的問題，如 Fig. 2c。

Fig. 2b 草繪了單極天線常見的參考面，可以看出單極天線只是雙極天線的變形。以拍手為例：單極天線就如同只有一隻手，必須拍在其他的物體如桌面才能發出聲音；聲音的大小和音質和物體特性有關。因此單極天線雖然簡單及應用廣泛，但特性常常會受到週遭物體的影響。

 

Fig. 2a and 2b

Fig. 2c

天線和 EMC

天線與 EMC 是一體兩面：EMC 的目標是減少或是消除 RF 雜訊的發射以避免干擾。綜上所述，任何天線都源自於有兩個導體的電位差。因此，避免 RF radiation 的方法就在於使兩個導體有相同的電位勢，沒有差異。注意是沒有電位差，但不一定需要接地。以拍手為例，就是把雙手綁在一起，就無法拍出聲。

 

Fig. 3

Fig. 3 草繪了一個常見的電子產品。電路板外有機殼，另有連外的傳輸線。如果傳輸線和機殼有電位差 (稱為 common mode voltage)，傳輸線就成為一個單極天線產生 RF 干擾，重點在於避免機殼和 common mode voltage 的電位差。

幾個 EMC 解決之道

如何連接機殼和內部電路參考電位(通常為 ground)非常重要。應該將 circuit ground 和機殼 ground 接點儘可能接近傳輸線接入電路的位置。並注意是否提供一個良好的 RF 低阻抗。任何在 circuit ground 和機殼 ground 之間的阻抗都會造成 RF 電位差而讓傳輸線變為天線。一般都是用金屬腳座或接地線做連結，並不能提供良好的 RF 低阻抗。

另一個方法是在傳輸線和機殼之間加入 RF bypass 電容降低  RF 的電位差。只是實際上也許不容易執行。

第三個方法是在傳輸線上加 common-mode choke 增加 common-mode 的阻抗，因而減少 radiation current。

最後，可能也是最有效的方式是直接在傳輸線上加 shielding 並適當的接在機殼上。

 

雙極和單極天線的電流分佈

假設我們用一個電流源, I, 灌入單極天線的基部，如 Fig. 4a 所示，頂部的電流為 0.  如果天線很短 (小於波長的 1/10)，電流的分佈接近線性，平均電流為 0.5I。如果天線較長（但小於波長的1/4) ，電流的分佈為 sinusoidal, 如 Fig. 4(b) 所示，平均電流為 0.68I。

  

Fig. 4a and 4b

因此，雙極和單極天線都並非均勻的 radiation，底部的 radiation 最大，頂部的 radiation 最小。比起理想的天線，短天線的平均 radiation 為 50%，長天線的平均 radiation 為 64%.  以上的例子同樣適用於 dipole 天線。

如何增加天線的效益？最簡單的方法就是增加平均電流。特別是增加天線頂部的電流。因為電流會經等效電容流入參考面，所以重點在於增加天線頂部到參考面的等效電容。

Fig. 5a and 5b

Fig. 5a 草繪一個"平頂天線"或電容式單極天線。藉著增加一個平頂可以增加頂部到參考面的電容，以增加天線的效率。平頂可以是任何形狀，金屬碟、線、球皆可。

Fig. 5b 草繪了一個應用同樣原理在雙極天線的例子，正如 Fig. 1c 的雙極天線。如果我們能增加到平均電流為 I, 天線的效益在短天線可以加倍；而 1/4 波長天線可以增加 36% 效益。

 

雙極和單極天線的電路模型

天線的實際應用一定需要週邊的線路。對於發射端，天線一般接在功率放大器 (PA) 之後。對於接收端，天線會接上 LNA。不論是發射或接收，最重要的特性就是阻抗匹配，才能達到最大的功率輸出或是最好的靈敏度。

因此，我們必須得到天線的等效電路，才能設計適當的匹配電路。綜合前幾節所述，等效電路中應含有電容。另外天線金屬線也必有電感。此外天線會 radiate 能量，一部份消失的能量也必須由這個簡單的 model 來解釋。唯一能消秏能量的元件是電阻，稱之為 "radiation resistance".  Fig. 6a 代表了一個簡化的雙極天線等效電路：串接的 R-L-C.

 

Fig. 6a and 6b: 雙極和單極天線的等效電路

在低頻時，這個等效電路如同電容而有高阻抗(>>100 Ohm)；到高頻時，等效電路如同電感而有高阻抗(>> 100 Ohm)。分界點是在共振頻率，等效電路是電阻而有低阻抗 (<100 Ohm)。

當然這是一個過份簡化的模型。很多其他的電路效應都沒有考慮其他 parasitic capacitance and inductance, skin effect 等等，但可以做為更複雜模型的基礎。

單極天線的阻抗是雙極天線的一半，可由 Fig. 6b 看出。這代表電阻和電感值是雙極天線的一半，但電容值是雙極天線的兩倍。

雙極和單極天線的共振頻率和天線的長度有關。對於雙極天線而言，1/2 波長為共振頻率，共振時的電阻為 72 Ohm. 對於單極天線而言，1/4 波長為共振頻率，共振時的電阻為 36 Ohm. 例如 10cm 長的單極天線，其共振頻率為 750MHz, 共振時的電阻為 36 Ohm.