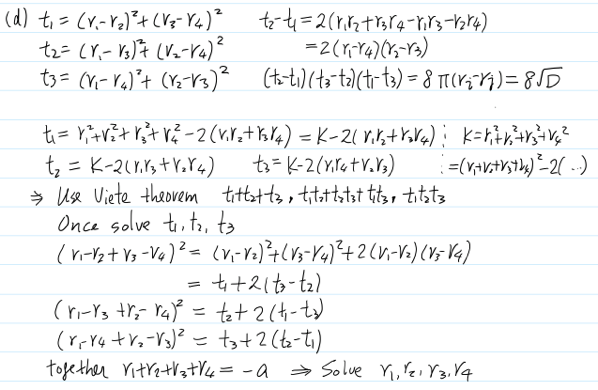Command Mode (press Esc to enable)
|
Edit Mode (press Enter to enable)
|
Allen Lu Advance
2017年6月23日 星期五
Jupyter Notebook Keyboard Shortcut
2017年6月9日 星期五
Matlab Advanced Data Structure
Reference:
http://blog.sina.com.cn/s/blog_4cf8aad30102wcu3.html
第一代的 matlab user (包含我)主要驚艷於 matrix (or vector, array) data type. 可以很方便做 matrix and vector operations. 特別是 element-wise operation (e.g. .* .^) 獨樹一幟,非常有用。但之後缺乏亮點,雖然也有 OOP matlab, 比起 python, caffe, tensorflow, 並沒有引起太大的注意 (at least for me).
隨著 machine learning and deep learning 變成主流應用。Matlab 終於找到新的舞台。除了提供相關的 toolbox, app, xxxLearner (e.g. ClassificationLearner), visualization tools 之外。也更新了 data structure and load function. 本文討論 Matlab advanced data structure.
Table
Matlab 2013b 引入新的 data structure 叫做 table. Table 類似 statistics toolbox 的 dataset. Table 的目的就是取代 dataset. Table 用於各類數據,比起 array 更廣泛。
2017年5月29日 星期一
漢語拼音
我的中文打字是從大易開始。當時大易是熱門的輸入法,和倉頡並列為最快的專業輸入法。大易和倉頡都是字根輸入法,有別於注音的拼音輸入法。
字根輸入法 pro: 不用選字,速度快。con: 必須記得所有字根。
拼音輸入法 pro: 只要記得發音,不需要記任何字型字根。con: 同音字很多。需要選字自然速度就慢。
不過風水輪流轉,拼音結合自動選字選詞,可以大幅加速輸入法的速度。
甚至只要打聲母就可以選詞。加上手機大多只支持拼音輸入法。
台灣最普遍的拼音就是注音輸入法,不用學就可用。不過我想挑戰自己。看老狗是否能學新把戲-漢語拼音。加上重新 refresh 注音。另外以後也可以看懂漢語拼音。
這篇文章就是用漢語拼音打成。
Step 1: 設定漢語拼音輸入法,但用繁體字型。
在Windows 裡其實已有內建漢語拼音輸入法,只要稍微變更下設定,便能輸出繁體中文字,不用再安裝其他的漢語拼音輸入法。
請參考本文。
Step 2: 最重要就是以下注音和漢語拼音對照表!!!!
https://hiraku.tw/2011/10/2784/

一xx => i xx
X xx => u xx
U xx => u xx
2017年5月7日 星期日
Google Cloud Platform GCP - Tensorflow Hello
本文介紹如何在 GCP install Anaconda and Tensorflow. 就我而言是最簡單的方式。
Step0: Create a VM (choose OS: Debian 8 或 Ubuntu TLS 14.04). 請參考前文。
Step1: Install Anaconda
Reference:
> mkdir downloads
> cd downloads
> wget http://repo.continuum.io/archive/Anaconda3-4.3.1-Linux-x86_64.sh
> bash Anaconda3-4.3.1-Linux-x86_64.sh
> source ~/.bashrc
2017/8/13 update
Anaconda update to 4.4.0 version
Step2: Install Tensorflow
Reference:
https://www.tensorflow.org/install/install_linux#InstallingAnaconda
Anaconda install Tensorflow 非常容易也非常快 (because of GCP?) !
> conda create -n tensorflow
> source activate tensorflow
再來是 install python tensorflow packages. 先 check python version: 3.6.0
(Tensorflow)$ > pip install --ignore-installed --upgrade \ https://storage.googleapis.com/tensorflow/linux/cpu/tensorflow-1.1.0-cp36-cp36m-linux_x86_64.whl
2017/8/13 update
Tensorflow update to 1.2.1 version
下一步是確認 tensorflow 是否 ok.
Run python
>>>import tensorflow as tf
>>> hello = tf.constant('Hello, TensorFlow!')
>>> sess = tf.Session()
>>>print(sess.run(hello))
Step3: Do a linear regression
參考以下 tutorial.
https://www.tensorflow.org/get_started/get_started
import numpy as np
import tensorflow as tf
# Model parameters
W = tf.Variable([.3], tf.float32)
b = tf.Variable([-.3], tf.float32)
# Model input and output
x = tf.placeholder(tf.float32)
linear_model = W * x + b
y = tf.placeholder(tf.float32)
# loss
loss = tf.reduce_sum(tf.square(linear_model - y))# sum of the squares
# optimizer
optimizer = tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
# training data
x_train =[1,2,3,4]
y_train =[0,-1,-2,-3]
# training loop
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)# reset values to wrong
for i in range(1000):
sess.run(train,{x:x_train, y:y_train})
# evaluate training accuracy
curr_W, curr_b, curr_loss = sess.run([W, b, loss],{x:x_train, y:y_train})
print("W: %s b: %s loss: %s"%(curr_W, curr_b, curr_loss))
2017年5月5日 星期五
Google Cloud Platform GCP - Tutorial
Google Cloud Platform 的 Quickstarts 蠻有參考價值。
https://cloud.google.com/getting-started/#ten-min-tutorial-section
Step1: Create a VM instance running Debian 8 OS
Step2: Install Apache(2) server and put /var/www/html/index.html
Step3: Try compute engine, 其實就是 step 1 + use python for a simple http server.
Step4: Try to run github sample code. I pick the Python Flask Skeleton for Google App Engine
(a) pip use apt-get (Debian) or yum (centos or redhat)
> sudo apt-get install python-pip
(b) install google cloud SDK 包含 gcloud, gsutil, bq, etc. command-line tools.
How? 可以參考 https://cloud.google.com/sdk/downloads
Download sdk.
Run install.sh
Initialize SDK: > sudo gcloud init
不過應該有更容易的方法 install Cloud SDK, to be checked.
(c) install App Engine Python SDK: How : > sudo gcloud components install app-engine-python
(d) > sudo gcloud components install app-engine-python-extras
接下來就是參考 git 的 tutorial
https://github.com/GoogleCloudPlatform/appengine-flask-skeleton
> sudo apt-get install git
> sudo git clone https://github.com/GoogleCloudPlatform/appengine-flask-skeleton.git
> cd appengine-flask-skeleton
> sudo pip install -r requirements.txt -t lib
不過 python 仍然有問題。這是 python 最麻煩的地方。要解決 packages 之間的相容性問題。一般需要 pip, virtualenv, etc. 請參考前文用 anaconda 解決 pip, virtualenv, 和相容性問題。
我找到一個很好的 blog.
Finally I made one work in “google Interactive Tutorial” 中的 “my-instance” VM.
I install anaconda2 and anaconda3, and tensor flow on anaconda3.
2017年5月1日 星期一
Google Cloud Platform for Machine Learning
之前在 linux (including using Raspberry pi) 作了一些 Machine Learning (ML) 的試驗。用了 OpenCV, Caffe.
自從 Google promote TensorFlow 之後。一直想再試一試。之前都是想用電競的主機或 notebook. 考慮價格高同時設定比較麻煩。因此開始留意幾家 cloud service providers.
包含 Google (Google Cloud Platform - GCP), Amazon (AWS), Ali (阿里雲), Microsoft (Azure).
最後選用 GCP 主要是 (1) TensorFlow 就是 Google 提供,相容性應該最好。 (2) 有 300 hour free trial.
I checked on the web, following the following link on Udacity example
Step 1.
Register in Google Cloud Platform -- easy if you have google account already.
Create a project : My First Project (default)
Step 2: Click on the "Activate Google Cloud Shell" on the top right button.
Step 3: in the shell window
List machine types:
> gcloud compute machine-types list
Step 4: Create an instance (VM?)
> gcloud compute instances create tf --image container-vm --zone asia-east1-c --machine-type n1-standard-2
=> tf is the name of the VM? (image container) The container-vm is deprecate.
=> asia-east1 can change to europe or us-west or us-east
=> n1 type computer and 2 CPUs
Step 5: copy a tensor flow example from Udacity
sudo docker run -d -p 8888:8888 --name tf b.gcr.io/tensorflow-udacity/assignments:0.5.0
Step 6: Find the instance in the dashboard and edit default network
Too hard to get it works.
Finally I made one work in “google Interactive Tutorial” 中的 “my-instance” VM.
I install anaconda2 and anaconda3, and tensor flow on anaconda3.
Back to wordpress first. 參考梅問題教學網
以下是 wordpress 的 ip address and paswd.
Finally I found the "Getting Started with Google Cloud Platform"
2016年11月7日 星期一
不用現代代數的 Galois Theory
現代代數在解釋 Galois Theory 大多是用 field/group 的 automorphism 和 homomorphism 解釋。
雖然簡潔優美,但缺乏直覺。其實 Galois 本身的思路是比較直覺容易理解。
前文提到結城浩的數學女孩就是 follow Galois 思路。雖然寫得很好,不過還是有些避重就輕。
雖然有解釋 Galois 的思路,但嚴謹度缺乏而顯得破碎。另一方面是缺少有分量的範例。
數學女孩大多用二次式來解釋。間或有三次以及四次的一些推論,但沒有札實的例子。
偏偏二次式是非常簡單的 case. 很難直觀推論到三次, 四次, 或五次方程式。
下文則是非常好的介紹文: Galois theory without abstract algebra. 也是同樣用 Galois 原來的思路。
同時輔佐實際的 2, 3, 4, 5 次式例子。即使五次式沒有通解。但 F20 group 仍存在根式解。
首先定義有理多項式(方程式)的根式解。如下:
A, B, C, D, 以及 a, b, c, .. 都是有理數。這是所謂的根式解。
二次式 x^2 + 2bx + c = 0 的根式解就是 1. A = b2 - c; B = -b; a = 1/2
三次式的根式解就是 2. 或是 2. 的 linear combination.
依此類推。
前文有提過上述根式解的數,都可以找到對應有理係數多項式的根。因此稱為代數數。
代數數的定義就是有理係數多項式的根。但並非所有代數數都可以
再來是定義 elementary symmetric polynomial
Elementary symmetric polynomial 就是把 (x+r1)(x+r2)(x+r3) ... (x+rn) 展開,根據 xi 項歸類所得的係數。
For example:
(x+r1)(x+r2) = x2 + σ1 x + σ2 where σ1 = r1 + r2 ; σ2 = r1 * r2
注意以上的公式適用於所有實數和複數,並無有理數的限制。
我們有興趣的 case 是有理數係數的多項式。當然根可能是或非有理數。但上述公式告訴我們。
根的 "基本對稱多項式" 如 σi 是有理數! 這是很直接但非常重要的觀察結果。
這個推論 (有理係數多項式的根所構成的基本對稱對項式是有理數) 能 extend 多遠?
相當遠! 可以証明任意有理對稱多項式滿足 Sn permutation invariant 結果都是有理數。同時可以表示為 σi 的有理式!
是用數學歸納法証明。
n=1 : σ1 = r1 ∈ Q. 任意有理(對稱)多項式 f(r1) = f(σ1) ∈ Q. 明顯成立。
假設 n-1 成立:
i.e. 任何有理多項式 f(r1, r2, ..., rn-1) = g(σ1, σ2, ..., σn-1) where f(r1, r2, ..., rn-1) is invariant under Sn-1 permutation
Prove n: for any rational symmetry polynomial f(r1, r2, ..., rn-1, rn) satisfy Sn permutation invariant.
First set rn = 0.
f(r1, r2, ..., rn-1, rn) = f(r1, r2, ..., rn-1, 0) 當然仍然滿足 Sn-1 permutation invariant.
By n-1 assumption, f(r1, r2, ..., rn-1, rn=0) = f(r1, r2, ..., rn-1, 0) = g(σ1, σ2, ..., σn-1, σn=0) from (6)
=> [f(r1, r2, ..., rn-1, rn) - g(σ1, σ2, ..., σn-1, σn)]rn=0 = 0 也就是 rn 是一個根。同理 r1, r2, ..., rn-1 都是根。
Clearly, f 1(r1, r2, ..., rn-1, rn) is invariant under Sn permutation. 同時比原來的 f 更低階。
我們可以重覆這個 operation. 一直到 f k(r1, r2, ..., rn-1, rn) = g(σ1, σ2, ..., σn-1, σn)
In summary
任意有理對稱多項式滿足 Sn permutation invariant 結果都是有理數。
同時可以表示為 σi (基本對稱多項式)的有理式!
Galois Group
Maximum group of roots permutation invariant under any function. The result is a known function of polynomial coefficients.
Example:
二次式 (roots: r1, r2):
σ1 = r1 + r2 , t2 = (r1 - r2)2 ∈ Q σ1 and t ∈ S2. t 開根號後可以計算 r1 and r2.
結果就是一開始的根式解。
至於 Galois group:
S2=C2=Z2 ⊳ E (The quotient group is Z2)
三次式 (roots: r1, r2, r3):
where α2 = ω, α3 = ω*ω
t1^3 is permutation invariant under A3. t2^3 is also permutation invariant under A3.
但是 t1^3+t2^3 and t1^3*t2^3 則是 permutation invariant under S3.
=> t1^3+t2^3, t1^3*t2^3 ∈ Q => 可以解出 t1 and t2 first.
=> 再由 t1 and t2 解出 r1, r2, and r3 by (15).
如何找 t1^3 and t2^3? 就是展開上式利用根和係數得到 t1^3+t2^3 and t1^3*t2^3
S3 ⊳ A3=C3=Z3 ⊳ E (The quotient group is Z2, and Z3, respectively)
四次式:
S4(24) ⊳ A4(12) ⊳ D2(4)=V4(4)=C2xC2 ⊳ C2=Z2(2) ⊳ E (The quotient group is Z2, Z3, Z2, and Z2 respectively)
同樣可以先解出
如同三次式的 t1^3 and t2^3! 當然 θ1 and θ2 滿足 A4 permutation invariant.
所以 θ1+θ2 和 (θ1-θ2)^2 滿足 S4 permuation invariant.
下一步就是要找到對應的 θ1 and θ2, 必須滿足 A4 permutation invariant.
(t1 + ω t2 + ω^2 t3)^3 = θ1
(t2 + ω t1 + ω^2 t3)^3 = θ2
(t1 + ω t3 + ω^2 t2)^3 = θ3 same as θ2, useless
t1 + t2 + t3 =?
看來只有 A3 permutation invariant?
但 t1, t2, and t3 不是四次式的根。而是三次式的根。不過是什麼三次式的根?
答案是 it depends:
如果定義 (a)
t1 = (r1+r2)(r3+r4)
t2 = (r1+r3)(r2+r4)
t3 = (r1+r4)(r2+r3)
可以得出一個三次式。
也可以定義 (b)
t1 = r1*r2 + r3*r4
t2 = r1*r3 + r2*r4
t3 = r1*r4 + r2*r3
可以得出另一個三次式。
t1 = [(r1-r2)(r3-r4)]^2
t2 = [(r1-r3)(r2-r4)]^2
t3 = [(r1-r4)(r2-r3)]^2
可以得出另一個三次式。
t1 = (r1-r2)^2 + (r3-r4)^2 = (r1-r2+ i r3 - i r4)*(r1-r2- i r3 + i r4) = (r1+ i*r3 -r2 - i*r4)(r1+ i*r4 -r2 - i*r3)
t2 = (r1-r3)^2 + (r2-r4)^2 = (r1-r3+ i r2 - i r4)*(r1-r3- i r2 + i r4) = (r1+ i*r2 -r3 - i*r4)(r1+ i*r4 -r3 - i*r2)
t3 = (r1-r4)^2 + (r2-r3)^2 = (r1-r4+ i r2 - i r3)*(r1-r4- i r2 + i r3) = (r1+ i*r2 -r4 - i*r3)(r1+ i*r3 -r4 - i*r2)
可以得出另一個三次式。
共同的特點 t1, t2, t3 都滿足 V8 (8) permutation invariant. Total 8*3 = 24 permutation 構成 S4 permutation invariant for t1+t2+t3, t1*t2+t2*t3+t3*t1, and t1*t2*t3.
藉著 S4 permutation invariant 代表三次方程式的係數都可由四次方程式的係數表示。
最常用的是 (a). 可以參考本文 for 三次式的 coefficient.
如果是 (d), 可以定義類似四次分圓根 (1,i,-1,-i) 的關係。
z1 = r1 + i r2 - r3 - i r4
z1' = r1 + i r4 - r3 - i r2
z2 = r3 + i r2 - r1 - i r4
z2' = r3 + i r4 - r1 - i r2
z3 = r2 + i r1 - r4 - i r3
z3' = r2 + i r3 - r4 - i r1
z4 = r4 + i r1 - r2 - i r3
z4' = r4 + i r3 - r2 - i r1
z1*z1' = z2*z2' = z3*z3' = z4*z4' = t1
同樣可以定義 t2 and t3.
t1+t2+t3 = (r1-r2)^2 + (r2-r3)^2 + (r3-r4)^2 + (r1-r3)^2 + (r1-r4)^2 + (r2-r4)^2
= 3*(r1+r2+r3+r4)^2 - 8*(r1r2+r1r3+r1r4+r2r3+r2r4+r3r4)
t1*t2+t2*t3+t1*t3 and t1*t2*t3 就要再計算。此處忽略。
先以 (a) 定義的三次多項式來看。
首先三次多項式的 D 和四次多項式的 D 是一致。其實 (a),(b),(c),(d) 都一致。
另外就是三次多項是否是 reducible? 也就是是否有有理根。
t1 = (r1+r2)(r3+r4)
r1+r2+r3+r4 = -a --- (1)
=> (r1+r2 - r3 - r4)^2 = a^2 - 4*t1
r1 + r2 - r3 - r4 = +/-sqrt(a^2 - 4*t1) --- (2)
r1 + r3 - r2 - r4 = +/-sqrt(a^2 - 4*t2) --- (3)
r1 + r4 - r2 - r3 = +/-sqrt(a^2 - 4*t3) --- (4)
From (1) to (4), we can solve r1, r2, r3, r4 unknowns.
也可以先解: r1+r2, r3+r4, r1+r3, r2+r4, r1+r4, r2+r3
從 r1+r2 只要有 r1-r2 就可解 r1, r2. r1-r2 = (r1+r3) - (r2+r3)
最後可解 r1, r2, r3, r4.
所以順序上是先解 θ1 and θ2. ( S4(24) ⊳ A4(12) )
再解 t1, t2, t3. ( A4(12) ⊳ V4(4) or S4(24) ⊳ V8(8) )
再解 r1+r2, r1+r3, r1+r4, r2+r3, r2+r4, r3+r4 ( V8(8) ⊳ C2(2) )
最後再解 C2(2) ⊳ E
-a3 = (r1+r2)+(r3+r4)
d1 = r1+r2 - (r3+r4) (12)(34)
d2 = (r1+r3) - (r2+r4)
d3 = (r1+r4) - (r2+r3)
(a3^2 - d1^2)/4 = (r1+r2)(r3+r4) = t1
(a3^2 - d2^2)/4 = (r1+r3)(r2+r4) = t2
(a3^2 - d3^2)/4 = (r1+r4)(r2+r3) = t3
實務上先做出一個三次方程預解式,使用 t1, t2, t3 為根。